1.基本原理：

光束在光纤中传输受到光纤数值孔径的限定，光纤数值孔径可表示为：

 

 

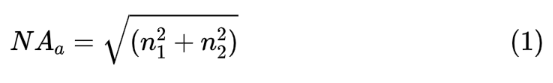
光束在透镜系统中传输受到透镜数值孔径的限定，透镜的数值孔径为：

 

 

其中,n1、n2为光纤芯层和包层的折射率，D 为透镜通光孔径，f为透镜的焦距。激光束通过耦合透镜进行聚焦，在焦平面上的分布仍呈高斯状分布，根据光束空间传输特性，焦平面上光斑的模场大小表示为：

 

 

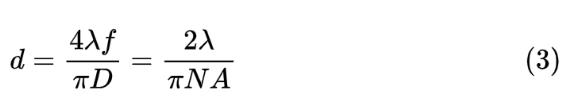
由此可见，耦合透镜的NA需要与光纤的NA完全匹配，才能实现空间光束到光纤的理想耦合。

 

 

图 1 空间光耦合到光纤基本原理图

 

       光纤耦合的基本原理如图1所示，在空间光通信中，接收到的激光束，经过整形系统后可近似看成平行光束，再通过聚焦透镜，在聚焦面上得到了经过傅里叶变换的爱里斑模场分布。耦合的基本原理是模式匹配，即爱里斑模场与单模光纤模场之间的匹配。由于通用光纤的模场是约定的，可以通过控制调节耦合透镜的相对孔径，使得聚焦光斑与光纤模场匹配，以实现高效率的光纤耦合。

 

2.光纤耦合效率

 

耦合效率η定义为耦合进光纤中的光功率与聚焦平面上接收的光功率P之比：

 

 

根据Parseval定理，入射光瞳面上与焦平面上计算耦合效率是等效的，由于入射光瞳面上的计算相对比较容易，因此在入射光瞳面上计算的η 为：

 

 

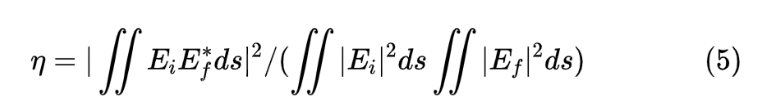
其中Ei为入瞳面光场,Ef为单模光纤模场在入射光瞳面时的等效模场，分布呈高斯形式：

 

 

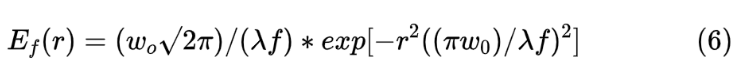
式中f光学系统焦距，ω0为单模光纤模场半径。结合上述两式，可以得到:

 

 

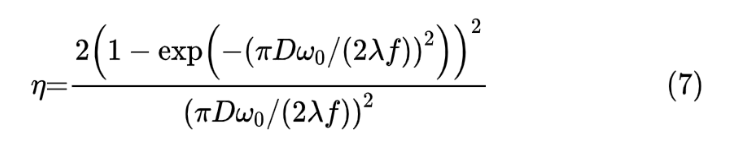
其中D为光束直径，得到了在理想条件下准直光束耦合进入单模光纤的耦合效率表达式。

       怎样实现最大的耦合效率一直是需要解决的问题，将自由空间光束耦合到单模光纤中时，虽然会存在不可避免地反射、散射和吸收损耗，但是最大的损耗来源于没有对准，或者说没有匹配到光纤准直器的工作模式。

       首先，一般来讲，光纤准直器（耦合头）的光束传播情况是我们需要耦合的空间光是标准高斯光束或者准高斯光束，所以光纤准直器在实际使用中需要特别关注高斯光束的束腰（或者称为腰斑）大小，即最小光束直径（或者半径）。光束从准直器输出后轻微汇聚到束腰，然后以相同速度发散，达到某一点后发散速度加快。由于高斯光束本身存在这样的性质，我们定义了瑞利长度：光束沿着其行进方向，从其束腰位置开始到其 倍束腰时的2倍距离。在瑞利长度内，我们默认光束是没有发散角的平行光。

 

图 2 光纤准直器/耦合头的腰斑（束腰）设计图示

 

       如上图所示，由于耦合的光束为高斯光束，光纤准直器/耦合头的设计原则遵循高斯光束的传输规则。由此带来不同束腰位置的设计，有些束腰位置位于会聚透镜上，有些则远离会聚透镜，但都在瑞利长度限度内。（一般光纤准直器/耦合头都会标明其束腰位置）

       了解光纤准直器/耦合头后，我们就可以将空间光耦合进光纤中。

 

 

图 3 透镜改变高斯光束腰斑位置和大小的示意图

 

       通过了解准直器/耦合头的设计束腰位置和大小，利用高斯光束的特性，就可以用透镜来实现不同高斯光束的空间重合——即腰斑位置和大小均在空间上重合（意味着无论传输多远，两束光在同一位置的光束直径都一致）。下面就是将空间光与光纤准直器/耦合头的设计腰斑及位置，利用透镜变换在空间上耦合起来，以此来达到光纤准直器/耦合头的理论耦合效率。